
https://www.acmicpc.net/problem/6588
6588번: 골드바흐의 추측
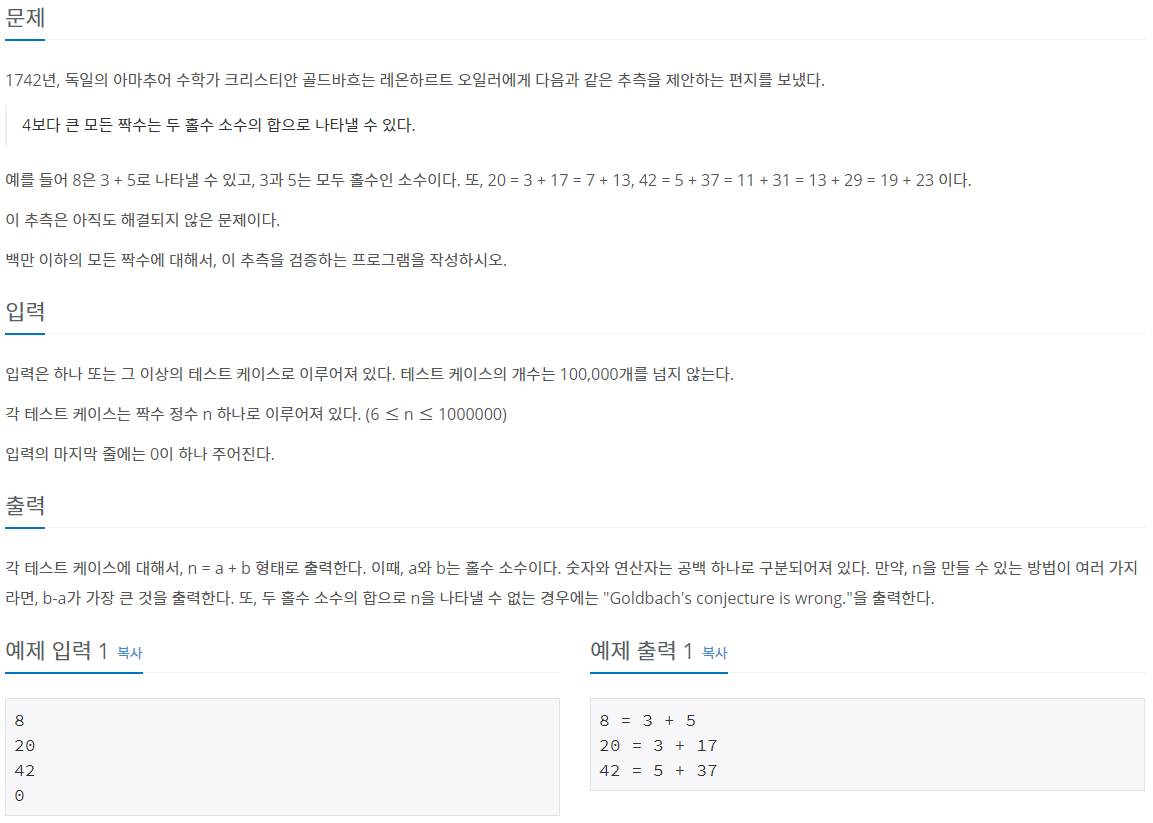
각 테스트 케이스에 대해서, n = a + b 형태로 출력한다. 이때, a와 b는 홀수 소수이다. 숫자와 연산자는 공백 하나로 구분되어져 있다. 만약, n을 만들 수 있는 방법이 여러 가지라면, b-a가 가장 큰
www.acmicpc.net
문제
21.03.05 접근법
- 입력 받으며 최댓값 찾기
- 최댓값까지만 소수 찾기 - 에라토스테네스의 체 사용
- 수가 소수들의 합인지 아닌지 판별 후, 찾으면 결과 출력 후 break와 ck=1
- 다 돌렸을 시, ck=0이면 소수들의 합으로 이뤄져 있지 않으므로 문구 출력
21.03.05 코드
1. 소수 판별에 list사용
제일 시간 적은 거
처음엔 dictionary를 사용했는데, 다른 사람들 시간을 보니깐 훨씬 짧아서 list를 사용해보니 반 이상으로 시간이 적게 나옴.
import sys
arr=[]
n=int(input())
maxNum=n
while n!=0:
arr.append(n)
n=int(sys.stdin.readline().strip())
if maxNum<n:
maxNum=n
prime=[1]*(maxNum+1)
prime[1]=0
for i in range(2,int(maxNum**0.5)+1):
for j in range(i+i,maxNum+1,i):
if prime[i]:
prime[j]=0
for i in arr:
ck=0
for j in range(2,int(i//2)+1):
if prime[j] and prime[i-j]:
print(i,'=',j,'+',i-j)
ck=1
break
if ck==0:
print("Goldbach's conjecture is wrong.")
2. 소수 판별을 dictionary사용
import sys
arr=[]
n=int(input())
maxNum=n
while n!=0:
arr.append(n)
n=int(sys.stdin.readline().strip())
if maxNum<n:
maxNum=n
prime={1:False}
for i in range(2,maxNum+1):
prime[i]=True
for i in range(2,int(maxNum**0.5)+1):
for j in range(i+i,maxNum+1,i):
if prime[i]==True:
prime[j]=False
for i in arr:
ck=0
for j in range(2,int(i//2)+1):
if prime[j]==True and prime[i-j]==True:
print(i,'=',j,'+',i-j)
ck=1
break
if ck==0:
print("Goldbach's conjecture is wrong.")
참고
최댓값 찾아서 소수를 하는 것보다 그냥 1000000까지 소수를 찾고, 한 반복문 안에서 수를 입력 받고 찾는 게 더 빠를 수도 있을까 해서 테스트를 해보았더니, 더 느림. 하지만, 메모리는 더 작았음.
import sys
prime={1:False}
for i in range(2,1000001):
prime[i]=True
for i in range(2,int(1000000**0.5)+1):
for j in range(i+i,1000001,i):
if prime[i]==True:
prime[j]=False
n=int(input())
while n!=0:
ck=0
for i in range(2,int(n//2)+1):
if prime[i]==True and prime[n-i]==True:
print(n,'=',i,'+',n-i)
ck=1
break
if ck==0:
print("Goldbach's conjecture is wrong.")
n=int(sys.stdin.readline().strip())
21.08.18 접근법
1. 한 번에 입력받아 저장하며 최댓값 동시에 구하기
2. 최댓값까지 소수 구하기
3. 소수들의 합인지 판별
# 무조건 deque쓰는 게 빠른 건 아니라는 결론! 때에 맞게 사용하기
소수구할 때 deque로 하면 시간초과남. 아마, 리스트로 True를 입력받아 deque로 변환하기에 더 오래걸리는 거 같음.
# max함수 사용보단 입력받으며 바로 비교할 것
# 앞에서부터 찾아가니깐 맨 처음에 찾은 값이 제일 차가 큰 값!
문제에서 "만약, n을 만들 수 있는 방법이 여러 가지라면, b-a가 가장 큰 것을 출력한다."로 끝까지 돌리고 차가 큰 값을 골랐었는데 시간초과..
저걸 제외하고 바로 소수들의 합이 발견되면 break를 거니 통과가 되었음.
21.08.18 코드
import sys
#값 입력받기
n=[]
nmax=0
while True:
_=int(sys.stdin.readline())
if _==0:
break
else:
n.append(_)
if nmax<_:
nmax=_
#최댓값까지 소수 구하기
prime=[True]*(nmax+1)
prime[0]=prime[1]=0
for i in range(2,int(nmax**0.5)+1):
if prime[i]==True:
for j in range(i+i,nmax+1,i):
prime[j]=False
#답 구하기
for i in n:
ck=0
for j in range(2,int(i//2)+1):
if prime[j]==True and prime[i-j]==True:
print('%d = %d + %d'%(i,j,i-j))
ck=1
break
if ck==0:
print("Goldbach's conjecture is wrong.")
'코딩테스트 준비 > 백준' 카테고리의 다른 글
| [백준] 1676번 팩토리얼 0의 개수 - 파이썬(Python) (0) | 2021.08.19 |
|---|---|
| [백준] 10872번 팩토리얼 - 파이썬(Python) (0) | 2021.08.18 |
| [백준] 1929번 소수구하기 - 파이썬(Python) (0) | 2021.08.11 |
| [백준] 1978번 소수 찾기 - 파이썬(Python) (0) | 2021.08.10 |
| [백준] 1934번 최소공배수 - 파이썬(Python) (0) | 2021.08.09 |